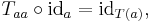Enriched category

In category theory and its applications to mathematics, enriched category is a generalization of category that abstracts the set of morphisms (hom-set) associated with every pair of objects to an opaque object in some fixed monoidal category of "hom-objects" and then defines composition and identity solely in terms of morphisms in the hom-object category. Enriched category theory thus encompasses within the same framework a wide variety of structures including

• ordinary categories in which the hom-set carries additional structure beyond being a set that needs to be preserved or otherwise accounted for (e.g., the existence of 2-cells between morphisms in a 2-category, or the addition operation on morphisms in an abelian category)
• category-like entities that don't themselves have any notion of individual morphism but whose hom-objects have similar compositional aspects (e.g., preorders where the composition rule ensures transitivity, or Lawvere's metric spaces, where the hom-objects are numerical distances and the composition rule provides the triangle inequality).

In the case where the hom-object category happens to be the monoidal category of sets and functions with the usual cartesian product, the definitions of enriched category, enriched functor, etc... reduce to the original definitions from ordinary category theory.

Enriched categories are also known as V-categories, this terminology being used in some influential texts like MacLane's; here V denotes the monoidal category of hom-objects.

Contents 1 Definition 2 Examples of enriched categories 3 Relationship with monoidal functors 4 Enriched functors 5 References

Definition

Let (M,⊗,I,, , ) be a monoidal category. Then an enriched category C (alternatively, in situations where the choice of monoidal category needs to be explicit, a category enriched over M, or M-category), consists of

• a class ob(C) of objects of C,
• an object C(a,b) of M for every pair of objects a,b in C,
• an arrow id_a:I → C(a,a) designating an identity for every object a in C, and
• an arrow °_abc:C(b,c)⊗C(a,b) → C(a,c) designating a composition for each triple of objects a,b,c in C,

such that the following three diagrams commute:

The first diagram expresses the associativity of composition.

Should it be the case that M is a category of sets and functions and (⊗,I,α,λ,ρ) is the usual monoidal structure (cartesian product, single-point set, etc.), each C(a,b) would then be a set whose elements are best thought of as "individual morphisms" of C while °, now a function, defines how consecutive such morphisms compose. In this case, each path leading to C(a,d) in the first diagram corresponds to one of the two ways of composing three consecutive individual morphisms from a → b → c → d from C(a,b),C(b,c) and C(c,d). Commutativity of the diagram is then merely the statement that both orders of composition give the same result, exactly as required for ordinary categories.

What is new here is that we have expressed this requirement without any explicit reference to individual morphisms in C — again, these diagrams are of morphisms in M, not C — thus making the concept of associativity of composition meaningful in the more general case where the hom-objects C(a,b) are abstract and C itself need not even have any notion of individual morphism.

Similarly, the second and third diagrams express the correponding identity rules:

If we again restrict ourselves to the case where M is a monoidal category of sets and functions, the morphisms id_a: I → C(a,a) become functions from the one-point set I and must then, for any given object a, identify a particular element of each set C(a,a), something we can then think of as the "identity morphism for a in C". Commutativity of the latter two diagrams is then the statement that compositions (as defined by the functions °) involving these distinguished individual "identity morphisms in C" behave exactly as per the identity rules for ordinary categories.

One should be careful to distinguish the different notions of "identity" being referenced here, e.g.,

• the monoidal identity I is an object of M, being an identity for ⊗ only in the monoid-theoretic sense, and even then only up to canonical isomorphism (λ, ρ).
• the identity morphisms 1_C(a,b):C(a,b) → C(a,b) which are actual morphisms that M has for each of its objects by virtue of it being (at least) an ordinary category.

from the morphisms id_a:I → C(a,a) that define the notion of identity for objects in the enriched category C, whether or not C can be considered to have individual morphisms of its own.

Examples of enriched categories

• Ordinary categories are categories enriched over (Set, ×, {•}), the category of sets with Cartesian product as the monoidal operation, as noted above.
• 2-Categories are categories enriched over Cat, the category of (small) categories and functors with monoidal structure being given by cartesian product. In this case the 2-cells between morphisms a → b and the vertical-composition rule that relates them correspond to the morphisms of the ordinary category C(a,b) and its own composition rule.
• Locally small categories are categories enriched over (SmSet, ×), the category of small sets with Cartesian product as the monoidal operation. (A locally small category is one whose hom-objects are small sets.)
• Locally finite categories, by analogy, are categories enriched over (FinSet, ×), the category of finite sets with Cartesian product as the monoidal operation.
• Preordered sets are categories enriched over a certain monoidal category, 2, consisting of two objects and a single nonidentity arrow between them that we can write as FALSE → TRUE, conjunction as the monoid operation, and TRUE as its monoidal identity. The hom-objects 2(a,b) then simply deny or affirm a particular binary relation on the given pair of objects (a,b); for the sake of having more familiar notation we can write this relation as a≤b. The existence of the compositions and identity required for a category enriched over 2 immediately translate to the following axioms respectively

 b ≤ c and a ≤ b ⇒ a ≤ c    (transitivity)
 TRUE ⇒ a ≤ a     (reflexivity)

which are none other than the axioms for ≤ being a preorder. And since all diagrams in 2 commute, this is the sole content of the enriched category axioms for categories enriched over 2.

• William Lawvere's generalized metric spaces, also known as pseudoquasimetric spaces, are categories enriched over the nonnegative extended real numbers R^+∞, where the latter is given ordinary category structure via the inverse of its usual ordering (i.e., there exists a morphism r → s iff r ≥ s) and a monoidal structure via addition (+) and zero (0). The hom-objects R^+∞(a,b) are essentially distances d(a,b), and the existence of composition and identity translate to

 d(b,c) + d(a,b) ≥ d(a,c)   (triangle inequality)
 0 ≥ d(a,a) 

• Categories with zero morphisms are categories enriched over (Set*, ∧), the category of pointed sets with smash product as the monoidal operation; the special point of a hom-object Hom(A,B) corresponds to the zero morphism from A to B.
• Preadditive categories are categories enriched over (Ab, ⊗), the category of abelian groups with tensor product as the monoidal operation.

Relationship with monoidal functors

If there is a monoidal functor from a monoidal category M to a monoidal category N, then any category enriched over M can be reinterpreted as a category enriched over N. Every monoidal category M has a monoidal functor M(I, –) to the category of sets, so any enriched category has an underlying ordinary category. In many examples (such as those above) this functor is faithful, so a category enriched over M can be described as an ordinary category with certain additional structure or properties.

Enriched functors

An enriched functor is the appropriate generalization of the notion of a functor to enriched categories. Enriched functors are then maps between enriched categories which respect the enriched structure.

If C and D are M-categories (that is, categories enriched over monoidal category M), an M-enriched functor T: C → D is a map which assigns to each object of C an object of D and for each pair of objects a and b in C provides a morphism in M T_ab: C(a,b) → D(T(a),T(b)) between the hom-objects of C and D (which are objects in M), satisfying enriched versions of the axioms of a functor, viz preservation of identity and composition.

Because the hom-objects need not be sets in an enriched category, one cannot speak of a particular morphism. There is no longer any notion of an identity morphism, nor of a particular composition of two morphisms. Instead, morphisms from the unit to a hom-object should be thought of as selecting an identity and morphisms from the monoidal product should be thought of as composition. The usual functorial axioms are replaced with corresponding commutative diagrams involving these morphisms.

In detail, one has that the diagram

commutes, which amounts to the equation

where I is the unit object of M. This is analogous to the rule F(id_a) = id_F(a) for ordinary functors. Additionally, one demands that the diagram

commute, which is analogous to the rule F(fg)=F(f)F(g) for ordinary functors.

References

1. Kelly,G.M. "Basic Concepts of Enriched Category Theory", London Mathematical Society Lecture Note Series No.64 (C.U.P., 1982)
2. Mac Lane, Saunders (September 1998). Categories for the Working Mathematician (second ed.). Springer. ISBN 0-387-98403-8.  (Volume 5 in the series Graduate Texts in Mathematics)
3. Lawvere,F.W. "Metric Spaces, Generalized Logic, and Closed Categories", Reprints in Theory and Applications of Categories, No. 1, 2002, pp. 1–37.